
What did you find for the values of \(2^0\) and \(5^0\) ?
Negative exponents fractions how to#
How to Divide Negative Exponents?ĭividing exponents with the same base results in the subtraction of exponents. This results in 16/9 which is the final answer. Then, find the value of the number by taking the positive value of the given negative exponent. How to Solve Fractions with Negative Exponents?įractions with negative exponents can be solved by taking the reciprocal of the fraction. There are two main rules that are helpful when dealing with negative exponents: For example, to solve: 3 -3 + 1/2 -4, first we change these to their reciprocal form: 1/3 3 + 2 4, then simplify 1/27 + 16. Negative exponents are calculated using the same laws of exponents that are used to solve positive exponents. For example, 2 -3 = 1/8, which is a positive number. No, it is not necessary that negative exponents give negative numbers. Do negative exponents Result in Negative Numbers? For example, in the number 2 -8, -8 is the negative exponent of base 2. The negative exponents mean the negative numbers that are present in place of exponents. The relation between the exponent (positive powers) and the negative exponent (negative power) is expressed as a x=1/a -xįAQs on Negative Exponents What do Negative Exponents Mean?.a -n is also known as the multiplicative inverse of a n.Exponent or power means the number of times the base needs to be multiplied by itself.Use the rule: a m × a n = a (m+n) to combine the common base (7).The first step is to write the expression in its reciprocal form, which changes the negative exponent to a positive one: (5/4) 3 × (3/10) 2.Let us understand the multiplication of negative exponents with the following example. After this conversion, we multiply negative exponents using the same multiplication rule that we apply for multiplying positive exponents. As we have already discussed that negative exponents can be expressed as fractions, so they can easily be solved after they are converted to fractions. Multiplication of negative exponents is the same as the multiplication of any other number. Use the second rule with a negative exponent in the denominator: 1/a -n =a n.Take the Least Common Multiple (LCM): (9 + 4)/36 = 13/36.Use the negative exponent rule a -n = 1/a n.Let us apply these rules and see how they work with numbers.

Rule 2: The rule is the same even when there is a negative exponent in the denominator.Rule 1: The negative exponent rule states that for a base 'a' with the negative exponent -n, take the reciprocal of the base (which is 1/a) and multiply it by itself n times.
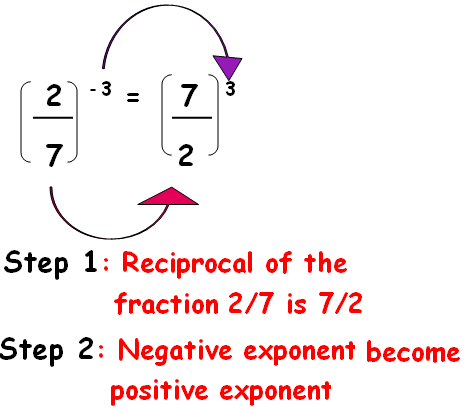
Given below are the basic rules for solving negative exponents. We have a set of rules or laws for negative exponents which make the process of simplification easy.


 0 kommentar(er)
0 kommentar(er)
